Chega aquela época do campeonato brasileiro em que se começa a falar em probabilidade de vitória. Ouvi alguém comentar que as chances do Cruzeiro ganhar o campeonato são de 85%.

Como fazem isso? Simples: Cada jogo tem 3 possibilidades: Time A, Empate, Time B. São 10 jogos por rodada, então cada rodada tem 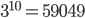diferentes combinações de resultado possíveis. Bastaria enumerar todos os cenários possíveis das 6 rodadas restantes e contar em quantos % deles o time 1 é campeão, em quantos o time 2 é campeão e assim por diante.

Ainda é uma quantidade astronômica de cenários a serem contatos (lembrando que são 6 rodadas, então são 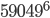diferentes possíveis maneiras do campeonato terminar a partir de agora, um número de 48 dígitos), mas não precisamos contar todos. À medida que o campeonato chega ao fim, poucos times têm pontuação suficiente para chegar ao topo, então podemos nos limitar aos times que poderiam ganhar o campeonato com os 18 pontos ainda em disputa. Hoje são apenas 7 times, ou 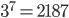cenários que precisam ser computados nesta rodada, porque nenhum dos outros dos 59k possíveis contribui para alterar o resultado final.

Assim dá para eliminar cenários “inúteis” para cada rodada futura e manter o tamanho da computação sob controle.

E é por isso que essas “probabilidades de vitória, libertadores ou queda” só aparecem no fim do campeonato. Temos 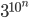possibilidades, onde n é o número de rodadas faltantes. Só quando n é pequeno e podemos reduzir aquele 10, eliminando times que não tem mais chances de ganhar, terminar no G4 ou cair é que se torna prático enumerar cenários e contar probabilidades.

Exceto, claro, na primeira rodada quando a chance de cada um dos 20 times é a mesma: 5%.

Anyway, não serve para muita coisa, exceto curiosidade e para dar assunto para comentaristas esportivos.